✌自旋极化单重态的介绍与使用
应用场景
(1)双自由基。两个单电子间作用不强时单重态往往比三重态能量要低。比如·CH2-CH2-CH2·、·O-O-O·,两边的单电子自旋相反。
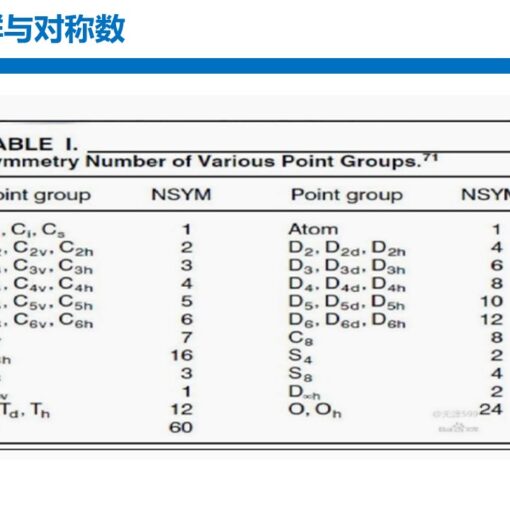
(2)反铁磁性耦合配合物。比如Mn2O2(NH3)8,基态是中性单重态,而两个Mn(II)在形式上都有5个d单电子,且在二者上的自旋相反。
(3)共价键被拉长的情况。在共价键处于平衡位置附近体系可完全以限制性波函数描述,而当拉长到一定距离后(称为不稳定点),对称破缺态的能量将比非破缺态要低。
(4)矩形有限尺寸石墨纳米带……
介绍
自旋极化单重态(对称破缺态)是一类特殊的单重态。但是量子化学程序会按照一般单重态处理,如果基态是极化单重态将无法得到基态,所以需要人为地提供一个合适的自旋极化的初猜波函数,才能收敛到真正的基态。
与单重态、多重态比较:
对于单重态,一般用限制性方法计算,即alpha和beta轨道完全匹配,自旋密度处处为0;
对于多重态,一般用非限制性方法计算,即alpha和beta轨道允许不匹配,不匹配程度(或称自旋极化程度)一般用它们之间重叠积分偏离1的程度衡量。
还有一类特殊的单重态,即自旋极化单重态,它是指体系自旋多重度为1,但是自旋密度并不处处为0的态有的地方alpha电密度大,有的地方beta电子密度大。输入文件推荐
%chk=name_stbopt.chk #自定义命名
%mem=8GB #内存与核时视情况而定
%nprocshared=8
#p stable=opt nosymm guess=mix def2tzvp um062x
第一步优化波函数 获得对称破缺态
放结构 举例:
0 1
C -0.12914200 0.37842100 -0.00004900
H -0.01333700 1.46460900 0.00010500
F 1.09094000 -0.19539000 0.00000900
O -1.12878400 -0.24707800 0.00001400
--Link1--
%oldchk=name_stbopt.chk
%chk=name_read.chk
%mem=8GB
%nprocshared=8
#p opt freq guess=read def2tzvp em=gd3 um062x
第二步优化和频率计算
放结构 举例:
0 1
C -0.12914200 0.37842100 -0.00004900
H -0.01333700 1.46460900 0.00010500
F 1.09094000 -0.19539000 0.00000900
O -1.12878400 -0.24707800 0.00001400
书写时需要注意:
(1)nosymm表示不对称,注意不要遗落
(2)对方法需要在前面添加u,表示开壳层如使用方法为m062x,这里则需要写成um062x
(3)两步中结构信息一致,第一步只是为获取对称破缺态的波函数,第二步则是在此基础上进行计算