辨析计算化学中的任务类型和理论方法

文/Sobereva@北京科音
First release: 2023-Aug-5 Last update: 2024-Dec-9

0 前言

在网上答疑时，偶尔看到有初学者搞不清楚任务类型和理论方法，比如今天有人在思想家公社3号群问"md，aimd和qmmm的区别是啥啊？什么需求下会用到这三种呢？"，这三个词明显都不是一个层面的东西。此文就把计算化学中的任务类型和理论方法的关系明确一下，简明扼要地介绍一下相关基本概念，做一个科普，以令计算化学零基础者一次性搞清楚它们的关系。

1 任务类型

有N个原子的非线型的体系有3N-6个内坐标描述原子间相对位置关系，在Born-Oppenheimer近似下体系的能量是依赖于内坐标的，也即能量是个3N-6维的函数，这被称为势能面（potential energy surface, PES）。计算化学领域有很多常见的任务（task）都是基于势能面做的，即有了势能面信息就能做这些任务。下面罗列常见的这种类型的任务：

常见任务类型：

• 优化极小点：
  平时说的几何优化（geometry optimization）一般也是指这个。此任务从一个给定的初猜结构开始，根据特定算法去寻找与之最近的势能面上极小点的精确位置。在分子动力学程序如GROMACS里这种任务也被叫做能量极小化（energy minimization, em），只不过实际目的不一样，em的目的主要是在动力学模拟之前释放体系中可能存在的较大斥力（自行构建的初始模型里往往有原子间距离太近、斥力太大），免得动力学模拟一开始由于过大的原子加速度造成过大的速度而导致动力学模拟异常或崩溃。

• 优化过渡态：
  从一个给定的初猜结构开始，根据特定算法去寻找与之最近的势能面上的一阶鞍点的精确位置。过渡态可以视为反应过程中最有代表性的一个结构，可以由此判断或验证反应机理，利用它和相邻极小点的能量求差可以得到反应势垒，对于讨论反应难易有关键意义

• 产生反应路径：
  用于把基元反应对应的势能面上两个相邻极小点之间最容易相互转变的路径产生，也相当于得到了一个轨迹并可以观看对应的结构变化过程，过渡态是此路径上能量最高点。在质量权重坐标下产生的反应路径称为IRC（intrinsic reaction coordinate），不考虑质量权重时产生的一般称为MEP（minimum energy path）。反应路径可认为是实际化学反应过程最有代表性的路径，自然对于理解反应机理有重要意义，还可以用Multiwfn对反应路径上各个点做波函数分析考察反应过程中电子结构的变化以获得更深入的信息。

• 振动分析：
  通常是在势能面上的驻点（所有原子受力都为0的点）做的，用于得到相应结构下的振动频率，可以用来计算热力学量，还可以用来得到振动能级、振动波函数、检验几何优化的准确性（根据虚频判断）、绘制振动光谱。

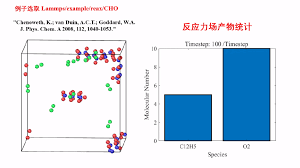
• 分子动力学（MD）：
  上面的任务都是“静态”的任务，即不含时间这个维度。而分子动力学则引入了时间这个维度，可以模拟体系状态随时间的变化，能研究的问题与那些静态的任务有极大的互补性。分子动力学模拟过程相当于体系在势能面上不断运动，也相当于是对势能面的一种采样方式。虽然其名字叫分子动力学，但研究对象并不限于分子，比如无机固体、金属团簇的动力学模拟也可以叫分子动力学。最常见的分子动力学的实现形式是BOMD（结合量子化学方法时另有CPMD、ADMP等），也相当于根据原子的位置、速度和受力按照经典牛顿运动方程演化原子的坐标和速度。还有其它一些特殊的动力学形式，如朗之万动力学、耗散粒子动力学等，如今用得很有限。

• 蒙特卡罗：
  和分子动力学并列的另一种常见的对势能面采样的方法，适用场合相对更少，主要是在多孔材料吸附小分子、计算气液共存曲线等问题上用得较多。不需要像MD那样计算受力和速度信息，也没有明确的时间的概念、无法像MD那样严格地考察含时演化。

• 构型/构象搜索：
  势能面上往往有很多极小点，能量最低的那个是全局最小点，可以视为体系最稳定的构型或构象对应的结构，其它的极小点对应亚稳的构型/构象。前面说的几何优化只能收敛到与初猜结构最近的极小点，显然这未必是最小点。如果想确保得到最小点（全局优化，global optimization），或者能量最低的一批构型/构象，就需要做构型/构象搜索，方法很多，比如免费的molclus就是很常用的实现工具。

波函数分析

• 用途广泛，包括：

  • 研究化学体系电子结构特征
  • 分析反应活性/位点/机理
  • 研究分子间和分子内弱相互作用
  • 分析电子激发
  • 研究分子性质和外场响应

• 常见分析方法：

  • Atoms-in-molecules (AIM)
  • Nature bond orbital (NBO)
  • 前线轨道理论
  • 概念密度泛函理论
  • 键级分析
  • 电子定域化函数（ELF）分析
  • 静电势/范德华势分析等

2 理论方法

分子力场

也称为经典力场（classical forcefield）或分子力学（molecular mechanics, MM），或者经验势函数等等。虽然通常带着“分子”俩字，但实际中不限于用于分子体系。这类方法一般使用简单的模型描述体系（通常一个原子作为一个粒子，电子与原子核不分开考虑），并用形式简单的数学函数（势函数）描述原子间相互作用。例如计算原子间静电相互作用时，分子力场普遍是给每个原子核位置分配一个点电荷（数值等于原子电荷），然后基于库仑公式计算。由于分子力场的形式简单，因此计算耗时极低。分子力场的一个关键的局限性是绝大多数分子力场都无法描述化学反应，因为成键关系在计算从始至终是固定不变的，是一开始就定义好的。描述化学反应问题主流的是后面提及的量子化学类型的方法，或者反应力场（远比普通分子力场要贵、支持的程序要少）。分子力场另一个关键局限性是依赖于大量参数，一方面影响模拟精度，一方面决定能描述的体系，寻找和构建合适的参数往往不是易事。

• 特点：
  • 使用简单模型描述体系
  • 采用简单数学函数描述原子间相互作用
  • 计算耗时极低
• 主要局限性：
  • 大多数无法描述化学反应
  • 依赖大量参数
  • 参数构建往往困难

机器学习势

• 基本思想：通过机器学习的思想构造依赖于原子坐标的分子描述符（如距离矩阵、能量矩阵等）与能量之间的抽象关系，这种关系比上述传统的分子力场用的势函数形式明显更为复杂。

量子化学方法类型：

密度泛函理论（DFT）

• 目前最普遍使用的理论方法
• 优势：
  • 性价比高
  • 精度良好
  • 普适性强
• 常见泛函：B3LYP、ωB97XD、PBE0、TPSS等
• 注意色散作用的处理

Hartree-Fock（HF）

• 已较为过时
• 耗时与DFT相近但精度较差

后HF方法

• 包括CCSD(T)、MP2、CISD等
• 在HF基础上考虑动态相关
• 耗时较高

MCSCF

• 主要弥补HF缺乏静态相关的考虑
• 最常见实现是CASSCF
• 对动态相关考虑有限

多参考方法

• 建立在MCSCF基础上
• 同时考虑动态相关和静态相关
• 典型方法：CASPT2、NEVPT2、MRCI
• 精度高但使用复杂且昂贵

半经验方法

• HF的简化版本
• 特点：
  • 耗时极低
  • 精度相对降低
  • 只适用于有限元素
• 典型方法：AM1、PM3、PM6

GFN-xTB

• 结合DFT思想的半经验级别方法
• 耗时与半经验相当
• 精度介于半经验和DFT之间

QM/MM方法

• 结合量子力学(QM)和分子力学(MM)的混合方法
• 特点：
  • QM部分：量子化学方法描述
  • MM部分：分子力场描述
  • 考虑两部分间的耦合
• 优势：
  • 相比全QM计算大幅降低计算成本
  • 可以重点关注关键区域
• 局限性：
  • MM区域精度较低
  • 多数情况下MM区域不能描述化学反应

基函数相关概念

• 基函数类型：

  • 原子中心基函数（如高斯型基函数）
  • 平面波基函数（主要用于周期性体系）

• 基组(basis set)：

  • 常见基组：6-31G*、def2-TZVP、cc-pVDZ等
  • 基组质量影响计算精度
  • 需要方法与基组相互匹配

3 任务类型与理论方法的结合

基本原则

• 各种理论方法原则上都可用于各种任务
• 具体组合取决于程序实现支持

特殊组合说明

AIMD和FPMD

• ab initio molecular dynamics (AIMD)
• first-principle molecular dynamics (FPMD)
• 区别：
  • AIMD主要用于孤立体系
  • FPMD主要用于周期性体系

QM/MM MD

• 结合QM/MM方法与分子动力学
• 优势：
  • 比全QM动力学计算更经济
  • 保持关键区域的精确描述
• 局限性：
  • MM区域描述相对粗糙
  • 需要合适的力场参数

激发态计算

• 可用专门的方法计算激发态：
  • TDDFT
  • EOM-CCSD等
• 注意事项：
  • 需考虑内转换、系间窜越等
  • 非绝热动力学需要额外算法
  • 实际应用比表面更复杂

参考来源

• 原始教程：计算化学公社